
Règles de l'astronomie siamoise
pour calculer les mouvements du Soleil et de la Lune,
traduites du siamois, et depuis examinées et expliquées par M. Cassini,
de l'Académie royale des Sciences.

M. de La Loubère, envoyé extraordinaire du roi à Siam, a rapporté un manuscrit siamois qui comprend des règles pour calculer les mouvements du Soleil et de la Lune selon la méthode de ce pays-là, et dont il m'a communiqué la traduction qu'il a aussi apportée de Siam. Cette méthode est extraordinaire. On ne s'y sert point de tables, mais seulement de l'addition, soustraction, multiplication et division de certains nombres dont on ne voit pas d'abord le fondement, ni à quoi ces nombres se rapportent.
On cache sous ces nombres diverses périodes d'années solaires, de mois lunaires et d'autres révolutions, et le rapport des unes avec les autres. On cache aussi sous ces nombres diverses espèces d'époques qu'on ne distingue point, comme l'époque civile, l'époque des mois lunaires, celle des équinoxes, celle des apogées et celle du cycle solaire. Les nombres dans lesquels consiste la différence entre ces époques ne sont pas ordinairement à la tête des opérations auxquelles ils servent, comme ils devraient être selon l'ordre naturel : ils sont souvent mêlés avec certains nombres, et les sommes ou les différences sont multipliées ou divisées par d'autres, car ce ne sont pas toujours des nombres simples, mais souvent ce sont des fractions tantôt simples, tantôt composées, sans être rangées en forme de fractions, le numérateur étant quelquefois dans un article et le dénominateur dans un autre, comme si l'on avait eu un dessein formé de cacher la nature et l'usage de ces nombres.
On entremêle au calcul du Soleil des choses qui n'appartiennent qu'à la Lune, et d'autres qui ne sont nécessaires ni à l'un ni à l'autre, sans en faire aucune distinction. On y confond ensemble des années solaires et des années lunisolaires, des mois de la Lune et des mois du Soleil, des mois civils et des mois astronomiques, des jours naturels et des jours artificiels. On y divise le zodiaque tantôt en douze signes selon le nombre des mois de l'année, tantôt en 27 parties selon le nombre des jours que la Lune parcourt le zodiaque, et tantôt en 30 parties selon le nombre des jours que la Lune retourne au Soleil. On n'y parle point d'heures dans la division du jour, mais il s'y trouve des 11e, des 703e et des 800e parties du jour, qui résultent des opérations arithmétiques que l'on prescrit.
Cette méthode est ingénieuse, et étant développée, rectifiée et purgée des choses superflues, elle sera de quelque utilité, se pouvant pratiquer sans livres, par le moyen de divers cycles et de la différence de leurs époques ; c'est pourquoi j'ai tâché de la déchiffrer, quelque difficulté que j'y aie trouvée d'abord, non seulement à cause de la confusion qui y règne partout et des noms qui manquent aux nombres supposés, mais aussi à cause des noms extraordinaires qu'on donne à ce qui résulte des opérations, dont il y en a plus de vingt qui n'ont pas été interprétés par le traducteur et dont je n'aurais jamais trouvé la signification si je n'avais auparavant découvert la méthode ; ce qui m'a aussi fait connaître que l'interprétation que le traducteur a faite de trois ou quatre autres noms n'est pas assez juste.
Dans cette recherche, j'ai distingué premièrement, et séparé des autres nombres, ceux qui appartiennent aux époques, ayant reconnu que ces nombres sont ceux que l'on donnait à ajouter ou à soustraire, ou simplement, ou en les divisant ou multipliant par certains autres nombres.
Secondement, j'ai considéré les analogies qui résultent des multiplications et divisions des autres nombres séparés des époques, et c'est dans les termes de ces analogies que j'ai trouvé les périodes des années, des mois, des jours, et les différences des unes aux autres, que l'expérience des choses astronomiques et l'occasion de diverses opérations que j'ai faites m'a fait reconnaître.
J'ai cru que les missionnaires, à qui l'astronomie donne entrée chez les grands et chez les savants par tout l'Orient, pourraient tirer quelque avantage de ce travail pour l'intelligence et pour l'explication de l'astronomie orientale, que l'on pourrait aisément rectifier et conformer à la nôtre sans apporter que très peu de changement à la méthode, en corrigeant les nombres dont elle se sert.
J'ai cru aussi qu'il ne serait pas inutile de réduire l'astronomie de l'Europe à cette forme, afin de s'en pouvoir servir au défaut des tables qui abrègent beaucoup le travail. Cette méthode serait bien plus facile à pratiquer dans la forme de l'année julienne et de la grégorienne dont nous nous servons, que dans la forme de l'année lunisolaire dont les Orientaux se servent ; car leur difficulté principale consiste à réduire les années lunisolaires et les mois lunaires civils aux années et aux mois du Soleil, que la forme de notre calendrier nous donne immédiatement, et ce qui m'a donné le plus de peine, ç'a été de reconnaître la méthode dont ils se servent pour les réduire, dans laquelle les diverses espèces d'années, de mois et même de jours, que l'on suppose que l'on cherche, ne sont point distinguées. C'est pourquoi on ne verra pas d'abord la raison de l'explication que je donne et de la détermination des genres aux espèces que je fais dans le commencement, mais on la comprendra dans la suite par la connexion des choses et par ce qui en résulte nécessairement.
De l'époque astronomique de cette méthode.
J'ai tâché de decouvrir quelle est l'époque d'où l'on commence à compter ici les mouvements du Soleil et de la Lune, et à quelle année, quel mois et quel jour de notre calendrier elle se rapporte, car il n'en est point parlé dans cet extrait, qui la suppose ou connue, ou expliquée peut-être dans les chapitres précédents du manuscrit d'où cet extrait a été tiré, puisque sans la connaissance de l'époque, il est absolument impossible de pratiquer cette méthode.
J'ai trouvé que cette époque est astronomique, et qu'elle est différente de la civile, ce que j'ai reconnu parce que l'on prescrit ici de commencer à compter les mois de l'année courante par le cinquième mois dans l'année embolismique qui est de 13 mois, et par le sixième mois dans l'année commune qui est de 12 mois. Car cela ne serait pas intelligible si l'on ne supposait deux différentes époques d'années, dont l'une, qui doit être l'astronomique, commence tantôt au cinquième, tantôt au sixième mois de l'autre, qui est la civile. Ce qui m'a fait encore connaître que l'époque astronomique est différente de l'époque civile, non seulement dans les mois, mais aussi dans les années, c'est l'opération que l'on fait ici pour trouver l'année de la naissance de quelqu'un, en soustrayant son âge du nombre des années échues depuis l'époque ; car cette opération serait inutile si l'on ne demandait que l'année de la naissance après l'époque civile que l'on connaît immédiatement, et que l'on compare à l'année courante pour savoir l'âge d'une personne.
Cela étant supposé, j'ai cherché premièrement le siècle auquel cette époque astronomique se peut rapporter, et ayant trouvé dans le calcul du Soleil fait par cette méthode, que deux signes et vingt degrés qu'on y emploie ne sauraient marquer que l'endroit du zodiaque où se trouvait l'apogée du soleil dans l'époque, lequel apogée devait être au vingtième degré des Gémeaux, j'ai jugé que cette époque devait être vers le septième siècle, où l'apogée du soleil se trouvait au vingtième degré des Gémeaux selon la plupart des tables astronomiques.
Secondement, ayant trouvé que le nombre 621, que l'on entremêle au calcul du Soleil, ne saurait être que le nombre de jours compris entre l'époque astronomique et le retour de l'apogée de la Lune au commencement du zodiaque, et que le nombre 3 232, que l'on y emploie ensuite, ne saurait être que le nombre des jours pendant lesquels cet apogée fait une révolution, j'ai établi que l'apogée de la Lune, qui en 621 jours fait deux signes et 9 degrés, était dans cette époque au 21e degré du Capricorne ; et parce que l'apogée de la Lune, par la révolution qu'il fait en 8 ans 2⁄3, retourne au même degré du zodiaque douze fois en un siècle, j'ai distingué les années du siècle auxquelles l'apogée de la Lune s'est trouvé en ce degré, et j'ai exclu les autres années.
Troisièmement, ayant trouvé par la manière dont on se sert ici pour calculer le lieu du Soleil, que cette époque astronomique est très proche de l'équinoxe moyen du printemps, qui au septième siècle arrivait le 20 ou 21 de mars, parmi ces années choisies, j'en ai cherché une dans laquelle l'apogée de la Lune arrivât à ce degré du Capricorne vers le 21 de mars, ce qui ne se rencontre qu'une fois en 62 années à quelques degrés près, et j'ai trouvé qu'en l'année 638 de Jésus-Christ, l'apogée de la Lune était au 11e degré du Capricorne le 21 de mars.
Quatrièmement, j'ai remarqué que cette époque astronomique doit avoir commencé à une nouvelle lune, parce qu'on réduit les mois lunaires en jours pour trouver le nombre des jours depuis l'époque, et la valeur des mois entiers étant otée de la somme des jours, le reste sert pour trouver la distance de la Lune au Soleil.
En l'année 638 de Jésus-Christ, la nouvelle lune équinoxiale arriva le 21 de mars à trois heures du matin à Siam, lorsque le Soleil, par son moyen mouvement, parcourait le premier degré d'Aries (1), l'apogée du soleil étant au 20e degré des Gémeaux, et celui de la Lune au 21e degré du Capricorne. Ce jour fut encore remarquable par une grande éclipse de soleil qui arriva le même jour, mais 14 heures après la conjonction moyenne.
Cinquièmement, par la manière de trouver le jour de la semaine qui est pratiquée ici, il paraît que le jour de l'époque fut un samedi, et le 21 de mars de l'an 638 fut aussi un samedi. Cela confirme encore la certitude de cette époque, et fait connaître le savoir et le jugement de ceux qui l'ont établie, qui se ne sont pas contentés d'une époque civile, comme ont fait les autres astronomes, mais qui en ont pris une astronomique, qui fût le principe naturel de plusieurs révolutions, lesquelles ne sauraient recommencer ensemble qu'après plusieurs siècles. Cette époque est éloignée de 5 ans et 287 jours de l'époque persienne de Jesdegerdes (2), dont la première année commence en l'an de Jésus-Christ 632 au 16 de juin. Ces règles indiennes, pourtant, ne sont pas tirées de tables persiennes rapportées par Crisococa (3), car ces tables font l'apogée du Soleil plus reculé de 2 degrés, et l'apogée de la Lune plus avancé de 6 degrés, ce qui ne s'accorde pas si bien avec nos tables modernes. Les tables persiennes font aussi l'équation du Soleil plus petite de douze minutes, et celle de la Lune plus grande de 4 minutes, ce qui s'accorde mieux avec les modernes.
Ces règles indiennes ne sont pas non plus tirées des tables de Ptolémée, où l'apogée du soleil est fixe au 5e degré et demi des Gémeaux, ni des autres tables faites depuis, qui font toutes cet apogée mobile. Il semble donc qu'elles ont été inventées par les Indiens, ou que peut-être elles ont été tirées de l'astronomie chinoise, comme on le pourrait conjecturer de ce que, dans cet extrait, les nombres sont écrits de haut en bas à la manière des Chinois ; mais il se peut faire que cette manière d'écrire les nombres soit commune à ces deux nations.
Ayant trouvé l'époque astronomique de cette méthode et le rapport qu'elle a avec les années juliennes, on peut rectifier les époques des mouvements du Soleil et de la Lune par les tables modernes, en ajoutant environ une minute par an à l'apogée du Soleil, et en corrigeant les autres périodes. Ainsi, il n'y aura plus de difficulté à réduire en jours les années et les mois depuis l'époque, et si l'on corrige aussi les équations conformément aux tables modernes, on trouvera par cette même méthode le lieu du Soleil et celui de la Lune avec beaucoup plus de justesse. Nous donnerons cette correction avec le supplément de ce qui manque à ces règles, après que nous les aurons expliquées.
| Règle pour trouver le lieu du Soleil de la Lune au temps de la naissance de quelqu'un. |
Explication
I
| 1e. Posez l' Ère. |
1e. L'Ère en ce lieu est le nombre des années depuis l'époque astronomique, d'où l'on prend le mouvement des planètes, jusqu'à l'année courante, qui paraîtra dans la suite.
| 2e. Soustrayez l'âge de la personne de l'Ère, vous aurez l'âge de la naissance. |
2e. L'âge de la personne est le nombre des années depuis sa naissance jusqu'à l'année courante, qui étant ôté de l' Ère, reste l'âge de la naissance, c'est-à-dire l'an depuis l'époque astronomique dans lequel la naissance est arrivée.
| 3e. Multipliez-la par 12. |
3e. En multipliant les années par 12, on les réduit en mois. Ces mois seront solaires, chacun de 30 jours 10 heures et demie, un peu plus ou un peu moins selon les diverses hypothèses, si les années sont solaires, ou à peu près si elles sont lunisolaires et en si grand nombre que l'excès des uns récompense le défaut des autres.
| 4e. Ajoutez-y le nombre des mois de l'année courante, et pour cela, si l'année courante est attikamaat, c'est-à-dire si elle a 13 mois de la Lune, vous commencerez à compter par le 5e mois ; que si elle n'est point attikamaat (4), vous commencerez à compter par le 6e mois. |
4e. La forme de l'année dont il s'agit ici est lunisolaire, puisqu'il y en a de communes de 12 mois lunaires, et d'abondantes ou embolismiques (5), appelées attikamaat, de 13 mois lunaires. De ce que l'on commence à compter les mois non par le premier mois de l'année, mais par le 5e, si l'année est embolismique, et par le 6e si l'année n'est pas embolismique, j'ai inféré qu'il y a deux époques et deux formes d'années différentes, l'une astronomique et l'autre civile ; que le 1er mois de l'année astronomique commence au 5e mois de l'année civile embolismique, qui serait le 6e mois sans l'insertion du mois embolismique qu'on ne compte point parmi les 12 mois et qu'on suppose être inséré auparavant ; et que dans les autres années, dont tous les mois sont comptés de suite sans intercalation, le 1er mois de l'année astronomique n'est compté qu'au 6e mois de l'année civile.
Mais comme l'on ne détermine pas ici expressément si on doit commencer à compter un mois entier au commencement ou à la fin du 5e ou du 6e mois, il se peut faire que l'on prenne pour 1er mois de l'année astronomique celui qui finit au commencement des mois dont il est parlé dans cet article. En ce cas, l'intervalle entre le commencement de l'année civile et le commencement de l'année astronomique ne serait que de 3 ou de 4 mois entiers, au lieu que si l'on ne compte un mois entier qu'à la fin du 5e ou du 6e mois, et que le premier mois que l'on compte selon cette règle soit le premier de l'année astronomique, l'intervalle entre les commencements de ces deux espèces d'années ne sera de 4 ou de 5 mois entiers. Nous verrons dans la suite que les Indiens ont diverses espèces d'années astronomiques, dont les commencements sont différents et ne sont pas beaucoup éloignés de l'équinoxe du printemps, au lieu que l'année civile doit commencer avant le solstice de l'hiver, tantôt au mois de novembre, tantôt au mois de décembre de l'année grégorienne.
On ajoute le nombre des mois de l'année courante, qui sont mois lunaires, à ceux qu'on a trouvés par l'article 3, qui sont mois solaires, et l'on suppose que la somme, toute hétérogène qu'elle est, soit égale au nombre des mois solaires échus depuis l'époque astronomique. On néglige la différence qu'il peut y avoir, qui en une année ne saurait monter à un mois entier, mais on pourrait s'y tromper d'un mois dans la suite des années si on ne prenait bien garde aux intercalations des mois, après lesquelles le nombre des mois que l'on compte dans l'année civile est plus petit que celui que l'on compterait sans les intercalations précédentes.
|
5e. Multipliez par 7 le nombre trouvé article 4.
6e. Divisez la somme par 228. 7e. Joignez le quotient de la division au nombre trouvé article 4. Cela vous donnera le maasaken (c'est-à-dire le nombre des mois) que vous garderez. |
5e, 6e, 7e. On cherche ici le nombre des mois lunaires depuis l'époque astronomique dont on a parlé à l'article 1 jusqu'au commencement du mois courant, ce que l'on fait en réduisant les mois solaires que l'on suppose avoir été trouvés ci-dessus, en mois lunaires, par le moyen de la différence qui est entre les uns et les autres. Dans les opérations que l'on fait, on suppose que comme 228 est à 7, ainsi le nombre des mois solaires donné est à la différence dont le nombre des mois lunaires surpasse le nombre donné des mois solaires écoulés pendant le même espace de temps ; qu'ainsi, en 228 mois solaires, qui font 19 années, il y a 228 mois lunaires et 7 mois de plus, c'est-à-dire 235 mois lunaires. Voici donc une période semblable à celle de Numa (6) et de Méton (7), et à notre cycle du Nombre d'or de 19 années pendant lesquelles la Lune se rejoint 235 fois au soleil.
Nous verrons néanmoins dans la suite que ces périodes, qui s'accordent ensemble dans le nombre des mois lunaires et des années solaires, ne s'accordent point dans le nombre des heures, à cause de la grandeur de l'année solaire et du mois lunaire, qui est supposée diverse dans ces diverses périodes, et que l'Indienne n'est point sujette à une faute si grande que le cycle ancien du Nombre d'or, qu'on a été obligé d'ôter du calendrier romain dans la correction grégorienne, parce qu'il donnait les nouvelles lunes plus tardives qu'elles ne sont à peu près d'un jour en 312 années, au lieu que les nouvelles lunes déterminées par cette période indienne s'accordent avec les véritables dans cet intervalle de temps à une heure près, comme l'on trouvera en comparant ces règles avec les suivantes.
II
|
1e. Posez le maasaken.
2e. Multipliez-le par 30. 3e. Joignez-y les jours du mois courant. |
On réduit ici les mois de la Lune en jours, mais parce qu'on fait tous les mois de 30 jours, ce ne seront que des mois artificiels plus longs d'environ 11 heures 16 minutes que les astronomiques, ou des jours artificiels qui commencent aux nouvelles lunes, et sont plus courts de 22 minutes 32 secondes que les jours naturels de 24 heures, qui commencent toujours au retour du soleil au même méridien.
|
4e. Multipliez le tout par 11.
5e. Ajoutez-y encore le nombre de 650. |
On réduit les jours en onzièmes de jour, en les multipliant par 11, et on y ajoute 650 onzièmes, qui font 59 jours et 1⁄11. Je trouve que ces 59 jours et 1⁄11 sont les jours artificiels, qui au jour de l'époque étaient échus depuis qu'une onzième partie de jour naturel, et une onzième de jour artificiel avaient commencé ensemble sous le méridien des Indes auxquels on accommode ces règles.
|
6e. Divisez le tout par 703.
7e. Gardez le numérateur que vous appellerez anamaan. 8e. Prenez le quotient de la fraction trouvée article 6, et le soustrayez du nombre trouvé article 3 ; le reste sera l'horoconne (c'est-à-dire le nombre des jours de l'Ère) que vous garderez. |
Ayant mis à part ce qu'on ajoute toujours par l'article 5, il paraît par la 2e, 3e, 4e, 6e et 8e opération, que comme 703 est à 11, ainsi le nombre des jours artificiels qui résulte des opérations de l'article 2 et 3 est au nombre des jours à rabattre pour avoir le nombre des jours naturels qui répond à ce nombre des jours artificiels : d'où il paraît qu'on faisant le mois lunaire de 30 jours artificiels, 703 de ces jours surpassent de onze jours le nombre des jours naturels qui les égalent.
On peut trouver la grandeur du mois lunaire qui résulte de cette hypothèse, car si 703 jours artificiels donnent un excès de 11 jours, 30 de ces jours, qui font un mois lunaire, donnent un excès de 30⁄703 de jour ; et comme 703 est à 330, ainsi 24 heures sont à 11 heures, 15 minutes, 57 secondes ; et ôtant de 30 jours cet excès, il reste 29 jours, 12 heures, 44 minutes, 3 secondes pour le mois lunaire, qui s'accorde à une seconde près au mois lunaire déterminé par nos astronomes.
À l'égard de la valeur de 59 jours et 1⁄11 que l'on ajoute avant la division, il paraît que si 703 jours donnent 11 à soustraire, 59 jours et 1⁄11 donnent 650⁄703 de jours, qui font 22 heures, 11 minutes et demie, dont la fin du jour artificiel a dû arriver avant la fin du jour naturel que l'on prit pour l'époque.
L'anamaan est le nombre des 703e parties de jour qui restent depuis la fin du jour artificiel jusqu'à la fin du jour naturel courant. On s'en sert dans la suite pour calculer le mouvement de la Lune, comme on l'expliquera ci-après.
Le quotient que l'on ôte du nombre des jours trouvé par l'article 3 est la différence des jours entiers, qui se trouve entre le nombre des jours artificiels et nombre des jours naturels depuis l'époque.
L'horoconne est le nombre des jours naturels échus depuis l'époque astronomique jusqu'au jour courant. Il semblerait qu'à la rigueur l'addition des jours du mois courant prescrite par l'article 3 ne se devrait faire qu'après la multiplication et la division qui sert à trouver la différence des jours artificiels aux jours naturels, parce que les jours du mois courant sont naturels, et non pas artificiels de 30 par mois. Mais on voit par la suite que cela se fait pour avoir avec plus de justesse l'anamaan qui sert au calcul du mouvement de la Lune.
III
|
1e. Posez l'horoconne.
2e. Divisez-le par 7. 3e. Le numérateur de la fraction est le jour de la semaine. |
Il suit de cette opération et de l'avertissement, que si après la division il reste 1, le jour courant sera un dimanche, et que s'il ne reste rien, ce sera un samedi : l'époque astronomique de l'horoconne est donc un samedi.
| Nota, Que le premier jour de la semaine est le dimanche. |
Si l'on sait d'ailleurs quel jour de la semaine est le jour courant, on verra si les opérations précédentes ont été bien faites.
IV
|
1e. Posez l'horoconne.
2e. Multipliez-le par 800. 3e. Soustrayez-en 373. 4e. Divisez-le par 292 207. 5e. Le quotient sera l'Ère, et le numérateur de la fraction sera le krommethiapponne que vous garderez. |
On réduit ici les jours en 800e de jour. Le nombre 373 de l'article 3 fait 373⁄800 de jour, qui font 11 heures et 11 minutes. Elles ne peuvent venir que de la différence des époques ou de quelque correction, puisque c'est toujours le même nombre que l'on soustrait. L'époque de cette section IV pourra donc être 11 heures et 11 minutes après la précédente.
L'Ère sera un nombre de périodes de jours depuis cette nouvelle époque, 800 desquelles feront 292 207 jours. La question est de savoir quelles seront ces périodes ? 800 années grégoriennes, qui approchent de fort près d'autant d'années solaires tropiques, font 292 194 jours. Si donc nous supposons que l'Ère soit le nombre des années solaires tropiques depuis l'époque, 800 de ces années seront trop longues de 13 jours selon la correction grégorienne.
Mais si nous supposons que ce soient des années anomalistiques (8) pendant lesquelles le Soleil retourne à son apogée, ou des années astrales pendant lesquelles le soleil retourne à la même étoile fixe, il n'y aura presque point d'erreur : car en 13 jours, qui est l'excès de 800 de ces périodes sur 800 années grégoriennes, le Soleil fait par son moyen mouvement 12°, 48', 48", que l'apogée du Soleil fait en 800 ans à raison de 57" 39‷ par an. Albategnius (9) fait le mouvement annuel de l'apogée du Soleil de 59" 4‷ et celui des étoiles fixes de 54" 34‷, et il y a des astronomes modernes qui font ce mouvement annuel de l'apogée du Soleil de 57", et celui des étoiles fixes de 51". Donc, si ce qui est ici appelé Ére est le nombre des années anomalistiques ou astrales, ces années seront à peu près conformes à celles qui sont établies par les astronomes anciens et modernes. Néanmoins, il paraît par les règles qui suivent, que l'on se sert de cette forme d'année comme si elle était la tropique, pendant laquelle le Soleil retourne au même lieu du zodiaque, et qu'on ne la distingue point des deux autres espèces d'années.
Le krommethiapponne qui reste après la division précédente, c'est-à-dire après avoir pris toutes les années entières depuis l'Époque, sera donc les 800e parties de jour qui restent après le retour du Soleil au même lieu du zodiaque ; et il paraît par les opérations suivantes que ce lieu était le commencement d'Aries. Ainsi, selon cette hypothèse, l'équinoxe moyen du printemps sera arrivé 11 heures 11' après l'époque de la section précédente.
V
|
1e. Posez le krommethiapponne.
2e. Soustrayez-en l'Ére. 3e. Divisez le reste par 2. 4e. Négligeant la fraction, soustrayez 2 du quotient. 5e. Divisez le reste par 7 : la fraction vous donnera le jour de la semaine. Nota, Que quand je dirai la fraction, je n'entends parler que du numérateur. |
Puisqu'à l'article 3 on a trouvé le jour de la semaine par l'horoconne d'une manière très facile, il est inutile de s'arrêter à celle-ci qui est plus longue et plus composée.
VI
|
1e. Horoconne.
2e. Soustrayez-en 621. 3e. Divisez le reste par 3 232. La fraction s'appelle outhiapponne, que vous garderez. |
Cette soustraction de 611 que l'on ôte toujours de l'horoconne, quelque nombre que l'horoconne contienne, marque une époque qui est 621 jours après l'époque de l'horoconne.
Le nombre 3 232 doit être le nombre des jours que l'apogée de la Lune emploie à parcourir le cercle du zodiaque, car 3 232 jours font 8 années juliennes et 310 jours. Pendant ce temps, cet apogée achève une révolution à raison de 6' 41" qu'il fait par jour, même selon les astronomes d'Europe. L'apogée de la Lune acheva par conséquent sa révolution 621 jours après l'époque de l'horoconne. On fait donc ici : Comme 3 232 jours sont à une révolution de l'apogée, ainsi le nombre des jours après l'époque de l'horoconne est au nombre des révolutions de l'apogée. On garde le reste, qui est le nombre des jours appelé outhiapponne. L'outhiapponne sera donc le nombre des jours échus depuis le retour de l'apogée de la Lune au commencement du zodiaque, ce qui paraîtra plus évidemment dans la suite.
|
Si vous voulez avoir le jour de la semaine par l'outhiapponne, prenez le quotient de la division susdite, multipliez-le par 5, puis joignez-le à l'outhiapponne, puis soustrayez-en 2 jours ; divisez par 7, la fraction marquera le jour.
Tout ce que dessus s'appelle poulasouriat, comme qui dirait la force du soleil. |
Ayant expliqué la vraie méthode de trouver le jour de la semaine, il est inutile de s'arrêter à celle-ci. On laisse le soin de l'examiner, et d'en chercher le fondement à ceux qui en auront la curiosité.
Nonobstant le nom de Force du Soleil que l'on donne ici aux opérations précédentes, il est constant que ce qui a été expliqué jusqu'à présent appartient non seulement au Soleil, mais aussi à la Lune.
VII
|
1e. Posez le krommethiapponne.
2e. Divisez-le par 24 350. 3e. Gardez le quotient qui sera le raasi, c'est-à-dire le signe où sera le Soleil. |
Pour trouver ce que c'est que le nombre 24 350, il faut considérer que le krommethiapponne sont les 800e parties de jour qui restent après le retour du Soleil au même lieu du zodiaque, et que l'année solaire contient 292 207 de ces parties, comme il a été dit dans l'explication de la section IV. La douzième partie d'une année contiendra donc 24 350 et 7⁄12 de ces 800e parties, c'est pourquoi le nombre 24 350 marque la 12e partie d'une année solaire pendant laquelle le Soleil par son moyen mouvement fait un signe.
Puisque donc 24350⁄800 de jour donnent un signe, le krommethiapponne divisé par 24 350 donnera au quotient les signes que le Soleil a parcouru depuis son retour par son moyen mouvement au même lieu : le raasi donc est le nombre des signes parcourus par le moyen mouvement du Soleil. On néglige ici la fraction 7⁄12, de sorte que l'année solaire reste ici de 292200⁄800, c'est-à-dire de 365 jours 1⁄4, comme l'année julienne.
|
4e. Posez la fraction de la division susdite, et la divisez par 811.
5e. Le quotient de la division sera le ongsaa, c'est-à-dire le degré où sera le Soleil. |
Puisque par l'article précédent, 24350⁄800 de jour donnent un signe du moyen mouvement du Soleil, la 30e partie de 24350⁄800 donnera un degré, qui est la 30e partie d'un signe. La 30e partie de 24 350 est 811 2⁄3, qui font un degré : divisant donc le reste par 811 2⁄3, on aura le degré du moyen mouvement du Soleil. On néglige ici les 2⁄3 qui ne peuvent faire une différence considérable.
|
6e. Posez la fraction de cette dernière division, et la divisez par 14.
7e. Le quotient sera le libedaa, c'est-à-dire la minute. 8e. Soustrayez 3 du libedaa. 9e. Mettez ce qui est au libedaa au-dessous de l'ongsaa, et l'<ongsaa au-dessous du raasi : cela fera une figure qui s'appellera le matteiomme du Soleil, que vous garderez : Je crois que c'est locus medius Solis. |
Puisque dans un degré il y a 811⁄800 parties, dans une minute, qui est la 60e partie d'un degré, il y aura 13 31⁄60 de ces parties. Négligeant la fraction, l'on prend le nombre 14, qui divisant le reste, donnera les minutes. La soustraction que l'on fait ici de 3 minutes est une réduction dont nous parlerons dans la suite.
On prescrit ici de mettre les degrés sous les signes, et les minutes sous les degrés en cette manière :
raasi, Signes.
ongsaa, degrés.
libedaa, minutes.
Cette disposition des signes, degrés et minutes l'un au-dessous de l'autre est appelée figure, et elle marque ici le lieu moyen du Soleil.
VIII
Pour trouver le vrai lieu du soleil.
|
1e. Posez le matteiomme du Soleil, c'est-à-dire la figure qui comprend ce qui est dans le raasi, le ongsaa et le libedaa.
2e. Soustrayez 2 du raasi. Que si cela ne se peut, ajouter 12 au raasi pour le pouvoir faire, puis le faites. 3e. Soustrayez 20 du ongsaa. Que si cela ne se peut, tirez 1 du raasi, qui vaudra 30 dans le ongsaa, puis vous tirerez le 20 susdit. |
Le nombre 2, que l'on soustrait du raasi dans l'article 2, et le nombre 20, que l'on soustrait de l'ongsaa dans l'article 3, sont 2 signes et 20 degrés qui marquent sans doute le lieu de l'apogée du Soleil selon cette hypothèse, dans laquelle on ne voit aucun nombre qui réponde au mouvement de l'apogée. Il paraît donc que cet apogée est supposé fixe au 20e degré des Gémeaux qui précède le lieu véritable de l'apogée, comme il est à présent, et 17 degrés, que cet apogée ne fait qu'en 1 000 ans, ou à peu près : d'où l'on peut juger que l'époque de cette méthode est environ mille ans avant le siècle présent. Mais comme la grandeur de l'année s'accorde mieux ici avec le retour du Soleil à l'apogée et aux étoiles fixes qu'avec le retour du Soleil aux équinoxes, il se peut faire que le commencement des signes dont on se sert ici ne soit plus présentement au point équinoxial, mais qu'il soit plus avancé de 17 ou 18 degrés, et ainsi il aura besoin d'être corrigé par l'anticipation des équinoxes. On soustrait donc ici l'apogée du soleil de son lieu moyen appelé matteiomme, pour avoir l'anomalie du Soleil, et le nombre des signes de cette anomalie est ce qu'on appelle kenne.
|
4e. Ce qui reste après cela s'appellera kenne.
5e. Si le kenne est 0, 1, ou 2, multipliez-le par 2 ; vous aurez le kanne. 6e. Si le kenne est 3, 4 ou 5, vous soustrairez la figure de cette figure ci : 5 29 60 qui s'appelle attathiat, et vaut 6 signes. 7e. Si le kenne est 6, 7, 8, soustrayez 6 du raasi, le reste sera le kanne. 8e. Si le kenne est 9, 10, 11, soustrayez la figure de cette figure-ci : 11 29 60 qui s'appelle Toüataasamounetonne, et vaut 12 signes : le reste dans le raasi sera le kanne. 9e. Si vous pouvez, tirez 15 du ongsaa ; ajoutez 1 au kanne : si vous ne pouvez point, n'y ajoutez rien. 10e. Multipliez le ongsaa par 60. 11e. Joignez-y le libedaa : cela sera le pouchalit, que vous garderez. 12e. Considérez le kanne. Si le kanne est 0, prenez le premier nombre du chaajaa du Soleil, qui est 35, et multipliez-le par le pouchalit. 13e. Si le kanne est quelque autre nombre, prenez selon le nombre, le nombre du chaiaa aatit, et le soustrayez du nombre du dessous ; puis ce qui restera dans le nombre du dessous, multipliez-en le pouchalit. Par exemple, si le kanne est 1, soustrayez 35 de 67, et du reste multipliez. Si le kanne est 2, soustrayez 67 de 94, et du reste multipliez le pouchalit. 14e. Divisez la somme du pouchalit multiplié par 900. 15e. Joignez le quotient au nombre supérieur du chaiaa dont vous vous êtes servi. 16e. Divisez la somme par 60. 17e. Le quotient sera ongsaa : la fraction sera le libedaa. Mettez un 0 au lieu du raasi. 18e. Mettez la figure trouvée par l'article précédent vis-à-vis du matteiommeMatthayom du Soleil. 19e. Considérez le ken de ci-dessus. Si le ken est 0, 1, 2, 3, 4, 5, il s'appelle ken soustrayant ; ainsi vous soustrairez la figure trouvée à l'article 17 du matteiomme du Soleil. 20e. Si le ken est 6, 7, 8, 9, 10, 11, il s'appelle ken ajoutant ; ainsi vous joindrez ladite figure au matteiomme du Soleil, ce qui vous donnera enfin le sommepont du Soleil que vous garderez précieusement. |
Il paraît par ces règles que le kanne est le nombre des demi-signes de la distance de l'apogée ou du périgée, prise selon la suite des signes selon que le Soleil est plus proche d'un terme que de l'autre ; de sorte qu'à l'article 5, on prend la distance de l'apogée selon la suite des signes, à l'article 6 la distance du périgée contre la suite des signes, à l'article 7 la distance du périgée selon la suite des signes, et à l'article 8 la distance de l'apogée contre la suite des signes. Dans les articles 6, 7, et 8, il semble qu'il faut toujours sous-entendre Multipliez le raasi par 2, comme il paraît dans la suite.
Dans l'article 6, quand les degrés de l'anomalie excèdent 15, on ajoute 1 au kanne, parce que le kanne, qui est un demi-signe, vaut 15 degrés.
On réduit ici les degrés et les minutes du kanne en minutes dont le nombre est appelé le pouchalit.
Il paraît par ces opérations, que le chaaaiaa est l'équation du Soleil calculée de 15 en 15 degrés, dont le premier nombre est 35, le second 67, le troisième 94, et que ce sont des minutes qui sont entre elles comme le sinus de 15, de 0 et de 45 degrés, d'où il s'ensuit que les équations de 60, 75 et 90 degrés sont 116, 129, 134, qui sont disposés à part en cette forme,
35
67
94
116
129
134
et répondent par ordre au nombre du kanne 1, 2, 3, 4, 5, 6. Pour les autres degrés, on prend la partie proportionnelle de la différence d'un nombre à l'autre, qui répond à 15 degrés qui font 900 minutes, faisant comme 900, à la différence de deux équations ; ainsi les minutes qui sont au surplus du kanne à la partie proportionnelle de l'équation, qu'il faut ajouter aux minutes qui répondent au kanne pour faire l'équation totale. On réduit ces minutes de l'quation en degrés et minutes, les divisant par 60. La plus grande équation du Soleil est ici de 2 degrés 12 minutes ; les tables alphonsines la font de 2 degrés 10 minutes ; nous la trouvons d'un degré 57 minutes. On applique l'équation au lieu moyen du Soleil pour avoir son vrai lieu qu'on appelle sommepont.
19e. Cette équation, conformément à la règle de nos astronomes dans le premier demi-cercle de l'anomalie, est soustractive, et dans le second demi-cercle, additive. On fait ici les opérations arithmétiques mettant l'un sous l'autre ce que nous mettons à côté, et au contraire mettant à côté ce que nous mettons l'un sous l'autre. Par exemple :
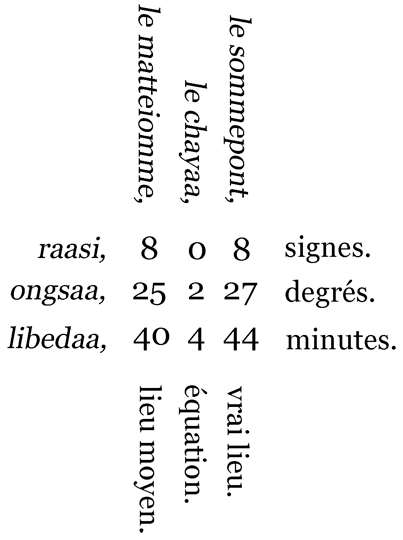
IX
|
1e. Posez le sommepont du Soleil.
2e. Multipliez par 30 ce qui est dans le raasi. 3e. Joignez-y ce qui est dans le ongsaa. 5e (10). Multipliez le tout par 60. 6e. Joignez-y ce qui est dans le libedaa. 7e. Divisez le tout par 800. Le quotient sera la reuc du Soleil. 8e. Divisez la fraction restante par 13. Le quotient sera le naati reuc que vous garderez au-dessous du reuc. |
Il paraît par ces opérations que les Indiens divisent le zodiaque en 27 parties égales, qui sont chacune de 13 degrés 40 minutes, car par les six premières opérations, on réduit les signes en degrés, et les minutes du vrai lieu du Soleil en minutes, et en les divisant après par 800, on les réduit en 27e parties de cercle ; car 800 minutes sont la 27e partie de 21 600 minutes qui sont dans le cercle ; on appelle donc reuc le nombre des 27e parties du zodiaque, dont chacune est de 800 kminutes, c'est-à-dire de 13 degrés, 40 minutes. Cette division est fondée sur le mouvement journalier de la Lune, qui est environ de 13 degrés, 40 minutes ; comme la division du zodiaque en 360 degrés a pour fondement le mouvement journalier du Soleil dans le zodiaque, qui est à peu près d'un degré.
La 60e de ces parties est 13 1⁄3, comme il paraît en divisant 800 par 60. C'est pourquoi on divise le reste par 13, négligeant la fraction, pour avoir ce qu'on appelle ici natireuc, qui sont les minutes ou 60e parties d'un reuc.
X
POUR LA LUNE
Pour trouver le matteiomme de la Lune
|
1e. Posez l'anamaan.
2e. Divisez-le par 25. 3e. Méprisez la fraction, et joignez le quotient avec l'anamaan. 4e. Divisez le tout par 60. Le quotient sera l'ongsaa, la fraction sera libedaa, et vous mettrez un 0 au raasi. |
Selon l'article 7 de la IIIe section, l'anamaan est le nombre des 703e parties de jour qui restent depuis la fin du jour artificiel jusqu'à la fin du jour naturel. Quoique selon cette règle, l'anamaan ne puisse jamais monter jusqu'à 703, néanmoins si l'on pose 703 pour l'anamaan, et qu'on le divise par 25, selon l'article 2, on a 28 13⁄25 pour le quotient. Ajoutant 28 à 703, selon l'article 3, la somme 731 sera un nombre de minutes de degré. Divisant 731 par 60, selon l'article 4, le quotient qui est 12° 11', est le moyen mouvement journalier par lequel la Lune s'éloigne du Soleil.
De ce qui a été dit dans les IIe section, il résulte qu'en 30 jours, l'anamaan augmente de 330. Divisant 330 par 25, on la dans le quotient 13 1⁄5. Ajoutant ce quotient à l'anamaan, la somme est 343, c'est-à-dire 5° 43' dont la Lune s'éloigne du Soleil en 30 jours, outre le cercle entier.
Les tables européanes font le mouvement journalier de 12° 11', et le moyen mouvement en 30 jours, de 5° 43' 21", outre le cercle entier.
|
5e. Posez autant de jours que vous en avez mis ci-desus au mois courant section II, n. 3.
6e. Multipliez ce nombre par 12. 7e. Divisez le tout par 30. Le quotient, mettez-le au raasi de la figure précédente qui a un 0 au raasi, et la fraction, joignez-la à l'ongsaa de la figure. 8e. Joignez toute cette figure au matteiomme du Soleil. 9e.Soustrayez 40 du libedaa. Que si cela ne se peut, vous tirerez 1 du ongsaa, qui vaudra 60 libedaa. 10e. ce qui restera dans la figure est le matteiomme de la Lune cherché. |
Après avoir trouvé les degrés et les minutes qui conviennent à l'anamaan, on cherche les signes et les degrés qui conviennent aux jours artificiels du mois courant. Car les multiplier par 12 et les diviser par 30, c'est la même chose que de dire : Si trente jours artificiels donnent 12 signes, que donneront les jours artificiels du mois courant ? On aura dans le quotient les signes. La fraction sont des 30e de signe, c'est-à-dire des degrés. On les joint donc aux degrés trouvés par l'anamaan, qui est l'excès des jours naturels sur les artificiels.
La figure dont il est parlé ici est la distance de la Lune au Soleil, après qu'on en a ôté 40 minutes, ce qui est ou une correction faite à l'époque, ou la réduction d'un méridien à un autre, comme on l'expliquera dans la suite. Cette distance de la Lune au Soleil étant ajoutée au lieu moyen du Soleil, donne le lieu moyen de la Lune.
XI
|
1e. Posez outhiapponne.
2e. Multipliez-le par 3. 3e. Divisez-le par 808. 4e. Mettez le quotient au raasi. 5e. Multipliez la fraction par 30. 6e. Divisez-la par 808. Le quotient sera ongsaa. 7e. Prenez la fraction restante, et la multipliez par 60. 8e. Divisez la somme par 808, le quotient sera libedaa. 9e. Ajoutez 2 au libedaa ; le raasi, l'ongsaa et le libedaa seront le matteiomme de iouthia, que vous garderez. |
Sur la section VI, on a remarqué que l'outhiapponne est le nombre des jours après le retour de l'apogée de la Lune qui se fait en 3 232 jours ; 808 jours sont donc la quatrième partie du temps de la révolution de l'apogée de la Lune, pendant lequel il fait 3 signes, qui sont la quatrième partie du cercle.
On trouve donc par ces opérations le mouvement de l'apogée de la Lune, faisant comme 808 jours sont à 3 signes ; ainsi le temps passé depuis le retour de l'apogée de la Lune est au mouvement du même apogée pendant ce temps. Il paraît par les opérations suivantes que ce mouvement se prend du même principe du zodiaque d'où l'on prend le mouvement du Soleil.
Donc, le matteiomme de iouthia est le lieu de l'apogée de la Lune.
XII
Pour le sommepont de la Lune
|
1e. Posez le matteiomme de la Lune.
2e. Posez vis-à-vis le matteiomme de iouthia. 3e. Soustrayez le matteiomme de iouthia du matteiomme de la Lune. 4e. Ce qui reste dans le raasi sera le kenne. 5e. Si le kenne est 0, 1, 2, multipliez-le par 2, ce sera le kanne. 6e. Si le ken est 3, 4, 5, soustrayez-le de cette figure-ci : 5 29 60 7e. Si le ken est 6, 7, 8, soustrayez-en 6. 8e. Si le ken est 9, 10, 11, soustrayez-le de cette figure-ci : 11 29 60. 9e. Si le kenne est 1 ou 2, multipliez-le par 2. Ce sera le Kanne. 10e. Tirez 15 du ongsaa, si cela se peut ; vous ajouterez 1 au raasi, sinon vous ne le ferez point. 11e. Multipliez l'ongsaa par 60, et joignez-y le libedaa, ce sera le pouchalit que vous garderez. 12e. Prenez dans le chaiaa de la Lune le nombre conformément au kanne, comme il a été dit du Soleil ; soustrayez le nombre de dessus de celui de dessous. 13e. Prenez le reste, et en multipliez le pouchalit. 14e. Divisez cela par 900. 15e. Joignez ce quotient au nombre de dessus du chaiaa de la Lune. 16e. Divisez cela par 60 : le quotient sera ongsaa, la fraction libedaa, et un 0 pour le raasi. 17e. Mettez vis-à-vis de cette figure le matteiomme de la Lune. 18e. Considérez le Ken. Si le Ken est 0, 1, 2, 3, 4, 5, soustrayez la figure du matteiomme de la Lune ; si le Ken est 6, 7, 8, 9, 10, 11, joignes les deux figures ensemble, et vous aurez le sommepont de la Lune, que vous garderez bien. |
Toutes ces règles sont conformes à celles de la section VIII pour trouver le lieu du Soleil, et s'entendent assez par l'explication faite de cette même section.
La différence n'est que dans le chaiaa de la Lune dont il est parlé ici à l'article 12 et 15. Ce chaiaa consiste dans ces nombres :
77
148
209
256
286
296
La plus grande équation de la Lune est donc de 4 degrés 56 minutes, comme la font quelques astronomes modernes, quoique la plupart la fassent de 5 degrés dans les conjonctions et dans les oppositions.
XIII
| Posez le sommepont de la Lune, et opérant comme vous avez fait au sommepont du Soleil, vous trouverez le reuc et le nattireuc de la Lune. |
Cette opération a été faite pour le Soleil à la section IX. Elle est pour trouver la position de la Lune dans les stations, qui sont les 27e parties du zodiaque.
XIV
|
1e. Posez le sommepont de la Lune.
2e. Mettez vis-à-vis le sommepont du Soleil. 3e. Soustrayez le sommepont du Soleil au sommepont de la Lune, et restera le pianne, que vous garderez. |
Le pianne est donc la distance de la Lune au Soleil.
XV
|
1e. Prenez le pianne et le posez.
2e. Multipliez le raasi par 30 ; joignez-y le ongsaa. 3e. Multipliez le tout par 60, et joignez-y le libedaa. 4e. Divisez le tout par 720, le quotient s'appelle itti, que vous garderez. 5e. Divisez la fraction par 12, le quotient sera natti itti. Fin du Souriat. |
Ces trois premières opérations servent à réduire en minutes la distance de la Lune au Soleil : la divisant par 720, on la réduit à des 30e parties de cercle, car 720 minutes font la 30e partie de 21 600 minutes qui font toute la circonférence. Le fondement de cette division est le mouvement journalier de la Lune au Soleil, qui est à peu près de la 30e partie de tout le cercle. On considère donc la position de la Lune, non seulement dans les signes et dans ses stations, mais aussi dans les 30e parties du zodiaque qui sont de 12 degrés chacune, et s'appellent itti ; divisant le reste par 12, on a les minutes ou les soixantièmes parties d'un itti, qui sont chacune de 12 minutes de degrés, dont la Lune s'éloigne du Soleil dans la soixantième partie d'un jour. Ces soixantièmes parties s'appellent natti itti.

NOTES
1 - Le Bélier, le premier signe du zodiaque. ⇑
2 - Yezdegerd (Yazdgard III, 624-651), empereur de Perse. Le début de son règne, le 16 juin 632, est la date initiale de l'ère qui porte son nom. ⇑
3 - Jorge Crisococas (Georges Chrysococcès), médecin et astronome byzantin du XIVe siècle. ⇑
4 - Nous donnons ci-dessous l'épellation des mots thaïs utilisés dans ce texte :
- Attikamat [athikamat] : อธิกมาส
- Maasaken [masaken]} : มาสเกณฑ์
- Anamaan [Anaman] : อนมาน
- Horoconne [Horakhun] : หรคุณ
- Krommethiaponne [kammachaphon] : กัมมัชพล
- Outhiaponne [utchaphon] : อุจจพล
- Poulasouriat [phon souriat] : พลสุริยยาตร์
- Raasi [Rasi] : ราศี
- Ongsaa [Ongsa] : องศา
- Libedaa [Lipda] : ลิปดา
- Matteiome [Matthayom] : มัธยม
- Kenne [ken] : เกนตร์
- Kanne [Khan] : ขันธ์
- Attathiat [Atthachakara] : อัฒจักร
- Pouchalit : ภุชลิบด์
- Toüataasamounetonne [Thawathasamonthon] : ทวาทศมณฑล
- Chaaja [Chaya] : ฉายา
- Chaiaa aattit [Chaya athit] : ฉายาอาทิตย์
- Sommepont [Somphut] : สมผุส
- Reuc [roek] : ฤกษ์
- Naati reuc [nathi roek] : นาทีฤกษ์
- Iouthia [ucha] : อุจจ์
- Pianne : เพียญชน์
- Itti [dithi] : ดิถี
- Naati itti [nathi dithi] : นาทีดิถี
5 - Dans le calendrier grec ancien et dans le calendrier israélite, se dit d'une année qui comporte un mois supplémentaire de trente jours, ou de ce mois lui-même, destiné à rétablir la concordance entre années lunaires et années solaires. (Larousse). ⇑
6 - Numa Pompilius, deuxième roi de la monarchie romaine ( -715 à -673). On lui attribue la réforme du calendrier romain, par le partage de l'année en douze mois lunaires et l'introduction de mois intercalaires pour correspondre à la durée de l'année solaire. (Wikipédia). ⇑
7 - Méton d'Athènes, astronome qui vécut dans la seconde moitié du Ve siècle av. J.-C. Il appliqua en -432 le fameux Cycle métonique, qui a pour base une somme de 235 lunaisons ou 6 940 jours, équivalent à 19 années solaires de 365 jours 5⁄19. (Wikipédia). ⇑
8 - Une année anomalistique est, en astronomie, la durée entre deux passages successifs de la Terre à son périhélie. (Wikipédia). ⇑
9 - Al-Battani (Abu Abdallah Muhammad Ibn Jabir Ibn Sinan Al-Battani Al-Harrani), astronome arabe du Xe siècle. ⇑
10 - Coquille ou omission, il n'y a pas d'article 4. ⇑

23 décembre 2019
